Math

Alright. So I'm taking advanced functions and I haven't done math for pretty much 2 years now and I need some help reviewing. So pretty much I know that there's 7 basic functions:
Linear
Quadratic
Rational
Square Root
Absolute Value
Exponential
Sinusoidal

Help that I need is remember how those last 5 work. I remember them slightly but yeah.... So I need help with the Rational, Square Root, Absolute Value, Exponential, and Sinusoidal. So can you guys throw me the formulas for those and maybe some examples?
Thanks.

PS please reply within the next day or two because my course moves quick and chances are that we'll be passed this part in the next class or two.

A rational function is any function that can be explained as a ratio of two polynomial functions [i.e. P(x) divided by Q(x)]. Someone check me on this, but I'm fairly sure that F(x) itself is a rational function, since you can divide it by 1. In comparison, irrational functions cannot be represented as the ratio of two polynomial functions [i.e. non-repeating, non-ending].

F(x) = (x - 1) / (x - 4) <-- Rational.
F(x) = (x - 1) / π <-- Irrational, since pi is an irrational constant.

Square root functions are functions of square roots. They have a positive domain so x cannot equal a negative number (unless, for example, you have the square root of x to a positive power, which would make a negative value positive anyway). Square root functions can be rational or irrational, since not all square root values can be defined as the ratio of two distinct numbers.

F(x) = √x
F(4) = √4
F(4) = 2 <-- Because you square 2 to get 4, so the square root of 4 is 2.

F(x) = √x(to the power of 4)
F(-3) = √-3(to the power of 4)
F(-3) = √81
F(-3) = 9 <-- Multiplying a negative number to a positive exponent works.

You shouldn't have the square root of a value to a positive exponent though anyway, since they'd cancel each other out. Absolute value functions are pretty simple. If you've got F(x) = |x| it just means that whatever you get between the two "|s" automatically becomes the absolute value, or positive value, when you're done working it out.

F(x) = |x - 4|
F(3) = |3 - 4|
F(3) = |-1|
F(3) = 1 <-- The absolute value of -1.

Exponential functions occur when a value is multiplied by a power including a variable. Logarithms are so much fun. Sinusoidal functions I'd never heard of by that name, but it looks like they're all functions involving trigonometric values (sine, cosine, etc) that create waves or wavelengths (so I think that rules out the tangent and cotangent, which have limits instead of continuous domains).

That good? Not sure how well I explained it all tbh. I haven't done math for several months before calculus class this semester, so this was a good review for me as well. What I'd like to know though, is what they call a function with more than one of these values. Like, the absolute value of a square root function to the power of five all divided by the cosine of x. Who wins?

erigons got it but its MATHS not math we created the english language so yer!

Yeah, but you guys never did get anything right on the first try. *jibe* We're just improvin' it.

Sinusoidal functions are like my life right now lol. So basically a sinusoidal function is a periodic function, periodic meaning that it repeats after a given period of time or with respect to whatever unit you are referring to.

So yes, Cosine and Sine functions are sinusoidal in nature.



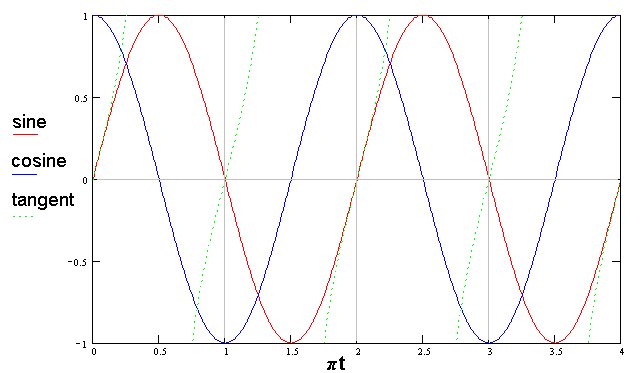
The difference between the Sine function and the Cosine function is that Cosine actually leads the Sine function by Pi/2 radians or 90 degrees. (2Pi radians = 360 degrees)

The equation to model a sinusoidal wave can be as such:

y(t) = A cos( wt + B ) + C

Where y(t) is the amplitude of the wave at a specific period of time, t.

A is the maximum positive or negative value from the offset value, C (generally C is equal to 0).

The value that determines how fast the function cycles through is w. The greater w is, the higher the frequency of the period is ( frequency is the inverse of the time it takes for the function to complete one period. ). w is generally multiplied by 2Pi so that it is converted into the unit of radians per second.

B is a constant generally and it offsets the phase of the function. It is typically in radians or degrees.

I think that should do it. I don't think you need to know leading and lagging functions or any of Euler's theorems on complex numbers...

Wow thanks a million every1! Especially Eregion u killed it !
U guys helped out a lot, u have no idea

Wow cool, maths i've never seen before!

Hai I maffs

Why won't my calculator give me an answer for πLn -1.

What's a TI-84 got that a TI-83 hasn't got.

*glowers at the calculator*

Maybe I've just got my settings messed or w/e.

My calculator wins. It's called a laptop. I can play Crysis on it with max settings.

holy shit.
im still on the 5+5 level.

So this is a week old topic but yeah...


Just though I'd mention that "Sinusoidal" functions (namely those dominated by a sin function) are really just exponentials, namely, a sum of exponentials, as can be seen doing a taylor expansion.

Most importantly, is Euler's (pronounced Oiler) formula, which states that e^(xi), where x is some angle, can be expressed as cos(x) + isin(x).

If you know how to work with complex numbers this makes trig identites MUCH easier.